Introduction
With this post, I would like to introduce an area of classical mechanics that most of you are probably not familiar with. Usually when we think of classical mechanics, Newton's laws of motion come to mind first. I'll show you a version or two of classical mechanics that make no mention of Newton's laws or even the concept of force (as a fundamental entity), and yet be completely equivalent in every sense with Newtonian mechanics. The benefits of these formulations will be made clear when we deal with them, but first we need some mathematical machinery: the calculus of variations. I'll focus on the ideas rather than the derivations and the proofs, showing only the important mathematical results.
The calculus of variations
It is said that the calculus of variations began with the brachistochrone problem, brachistochrone meaning "shortest time" in Ancient Greek.
Let two horizontally and vertically separated points P and Q be given in a plane with gravity acting downward. Find the curve joining the two points such that a bead starting from rest at the higher point will slide without friction along the curve and reach the lower point in the shortest possible time.
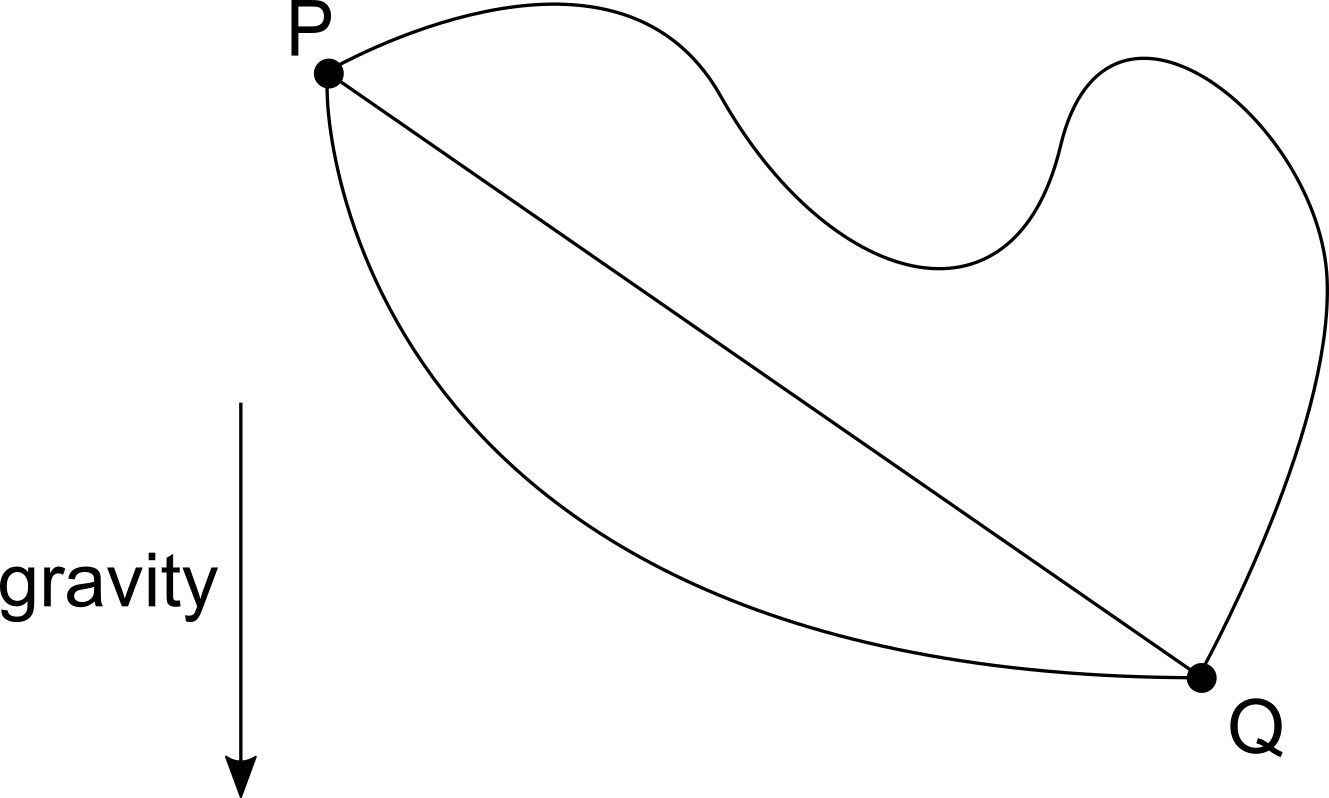
A simple illustration
What do you think is the answer to this problem? You might think it's the straight line connecting the two points, but remember, we want the curve that takes the shortest time and not the shortest distance. The solution is therefore not trivial. In fact, the solution is a cycloid connecting the two points. For more details, watch this great video from 3Blue1Brown and applied mathematician Steven Strogatz. They cover the history behind the problem and go into detail about its solution.
It was Leonard Euler who first gave a formal treatment of the subject of calculus of variations. Later, Lagrange gave a treatment dealing with many variables. The problem was to obtain the function for which a certain quantity is minimized or maximized. In the case of the brachistochrone problem, the quantity to be minimized was time and the function we wanted was that of the trajectory of the bead which had the least time. Notice how this is similar to finding the stationary points of a function, where it's the function which is either minimized or maximized by equating its derivative to zero. Indeed, we employ a similar method for this problem, where we're just finding the stationary function (rather than a point of some function) -- called the extremal -- from a set of functions. We'll now discuss these ideas in the context of physics, that is by assuming the dependent variables to be the position and velocity coordinates of a particle, and the independent variable being time. In general, these variables can be any function y1(x),y2(x),…, their derivatives y′1(x),y′2(x),…, for some independent variable x. The problem is this:
Given a function L of the positions q1,q2,…, (functions of time), velocities ˙q1,˙q2,…, (their derivatives) and time t (the independent variable), and the value of the positions at times t1 and t2 (the boundary conditions), what are the position coordinates for which the following integral is minimized (or made stationary)?
q(t) and ˙q(t) are vector functions representing all the corresponding position and velocity functions. The integral S[q(t)] is called the action and it is a function of functions, in particular the position functions. Functions of this form are called functionals and they map the input function onto a scalar. Now that we have set up the problem, it's time to jump into the domain of physics!
The principle of stationary action and Lagrange's equations
So why exactly do we want to find the positions for which the action is stationary? The answer lies in the principle of stationary action, the guiding variational principle behind the formulations of classical mechanics we're going to explore. It's more popularly called the principle of least action, but really the condition it imposes does not necessarily make the action least although in most situations it does:
The evolution of the system between the times t1 and t2 is given by the trajectory in configuration space for which the action S is stationary to first order.
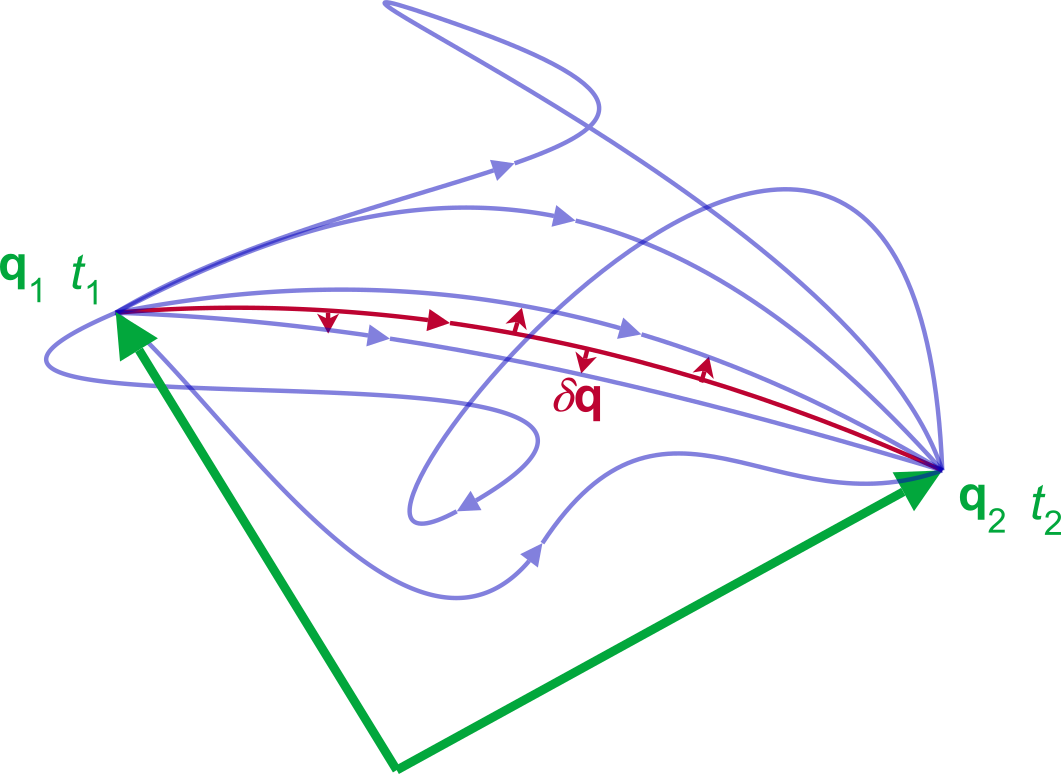
An illustration of the path of stationary action
In essence, what this means is that given two points, we have infinitely many possible trajectories passing through them. Which of these trajectories is the one taken by the system, and what distinguishes this trajectory from the others? The principle of stationary action says the trajectory with stationary action (or least action as is popularly stated) is the one describing the time evolution of the system. Putting δS = 0 yields the Euler-Lagrange equations, which are a set of differential equations that give the equations of motion when solved:
The function L(q,˙q,t) is called the Lagrangian of the system and it can usually be obtained through geometrical and physical considerations of the system. Once we know what L is, our system is completely solved by plugging it into the Euler-Lagrange equation. For conservative systems, finding the Lagrangian is rather straight forward because L = T − V, where T is the kinetic energy and V is the potential energy of the system.
What is the point of doing all this?
While this might seem like a lot of work for something that gives the same results as Newton's laws, the benefits come from the generality of Lagrange's equations. Newton's second law has the problem that it changes its form depending on the coordinates we use; it is not invariant under a transformation of coordinates. For example, it has one form when written with cartesian coordinates, but has a completely different form under polar coordinates and we need to do some vector analysis to go from one coordinate system to another. This problem does not arise in Lagrange's equations, which is invariant under a coordinate transformation. We're free to use any convenient set of coordinates depending on the symmetry of the system, and plug the Lagrangian into the Euler-Lagrange equations to get the equations of motion for that set of coordinates. One big advantage of this is that we can easily find the conserved quantities of the system, thus simplifying the problem. If the Lagrangian does not depend on some coordinate qi, then the momentum corresponding to that coordinate (called the conjugate momentum) is conserved. Such coordinates are called cyclic coordinates.
Thus, to summarise Lagrangian dynamics in a sentence, find the Lagrangian of the system and solve the Euler-Lagrange equations to get the equations of motion of the system. For simple systems, Newton's laws might be easy to apply, but it becomes very difficult as the systems get more complex, for example celestial systems. Lagrangian dynamics allows us to deal with these more complex systems. Apart from all of these conveniences, however, the principle of stationary action and its consequential formulations of classical mechanics have had far reaching influences on modern physics, including both Einstein's theory of relativity and quantum mechanics.
When I was in high school, my physics teacher—whose name was Mr. Bader—called me down one day after physics class and said, ‘You look bored; I want to tell you something interesting.’ Then he told me something which I found absolutely fascinating, and have, since then, always found fascinating. Every time the subject comes up, I work on it. In fact, when I began to prepare this lecture I found myself making more analyses on the thing. Instead of worrying about the lecture, I got involved in a new problem. The subject is this -- the principle of least action. -Richard Feynman, The Feynman Lectures on Physics Vol. II
In the next post, we shall explore Hamiltonian dynamics, which is yet another formulation of classical dynamics. What's special about Hamiltonian systems is that we can study their behaviour qualitatively without even solving for their equations of motions by analyzing them geometrically. It's quite brilliant.